LLM-FP4: 4-Bit Floating-Point Quantized Transformers
近年来,深度学习技术的飞速发展已经在各行各业得到了广泛应用。然而,深度学习模型通常需要大量的计算资源,这对于一些资源受限的场景来说是一个挑战。为了解决这个问题,我们提出了一种新的量化方法,即4位浮点量化,用于深度学习模型中的Transformer架构。文章发表在 Conference on Empirical Methods in Natural Language Processing (EMNLP) 2023上。
FP量化的准确度和exponent bits的设定以及量化的区间息息相关。不同的 FP format (浮点数的指数位 / 尾数位设定) 之间存在巨大的量化误差差异,只有当选取合适的 FP format 时,FP Quantization 比 INT Quantization 能更好的表示长尾分布。这个现象也在之前的论文中得到验证 [1]。为了解决这个问题,我们用一个 search-based 浮点量化算法,统筹搜索出最适合的浮点数的指数位 / 尾数位设定以及对应的量化区间。
此外,另一个同时出现在各种不同类别 Transformer 模型 (Bert,LLaMA,ViT) 中的现象也会严重影响量化的难度:那就是模型的 activation 中不同 channel 之间的数量级会有很高的差异,而同 channel 之间的量级十分一致。之前 LLM.int8 [2] 和 SmoothQuant [3] 也有类似的发现,不过我们发现这个现象不仅仅存在于 LLM 中,并且在其他 Transformer 模型里也有类似现象,LLaMA 与 BERT 以及 DeIT-S 中的 activation 的分布都发现了类似的现象。异常大的 channel 都比剩余的 channel 大很多,所以在量化 activation tensor 的过程中,量化的精度很大程度会被这些异常值决定,从而抑制其他 channel 值的量化区间,最终降低整体影响量化精度。这会导致量化的最终结果崩坏,尤其当比特数降到一定程度的时候。值得注意的是,只有 tensor-wise 和 token-wise 量化可以在 efficient matrix multipilication 的时候将 scaling factor 提取出来,而 channel-wise 量化是不支持 efficient matrix multipilication 的。
为了解决这个问题,同时维持高效率矩阵乘法 (Efficient Matrix Multiplication),本文利用少量的校正资料集,预先算出 activation 的每个 channel 的最大值,从而计算缩放因子。然后将这个缩放因子一拆为二,拆解成一个 per-tensor 的实数乘以 per-channel 的 2 的幂。而这个 2 的整数次方即用 FP 里的 exponent bias 表示。 进一步地,在 calibration 完成之后,这个 per-channel exponent bias 就不再变化,因此可以和 weight quantization 一起进行预计算 (pre-compute),将这个 per-channel exponent bias 整合进量化后的 weights 中,提高量化精度。
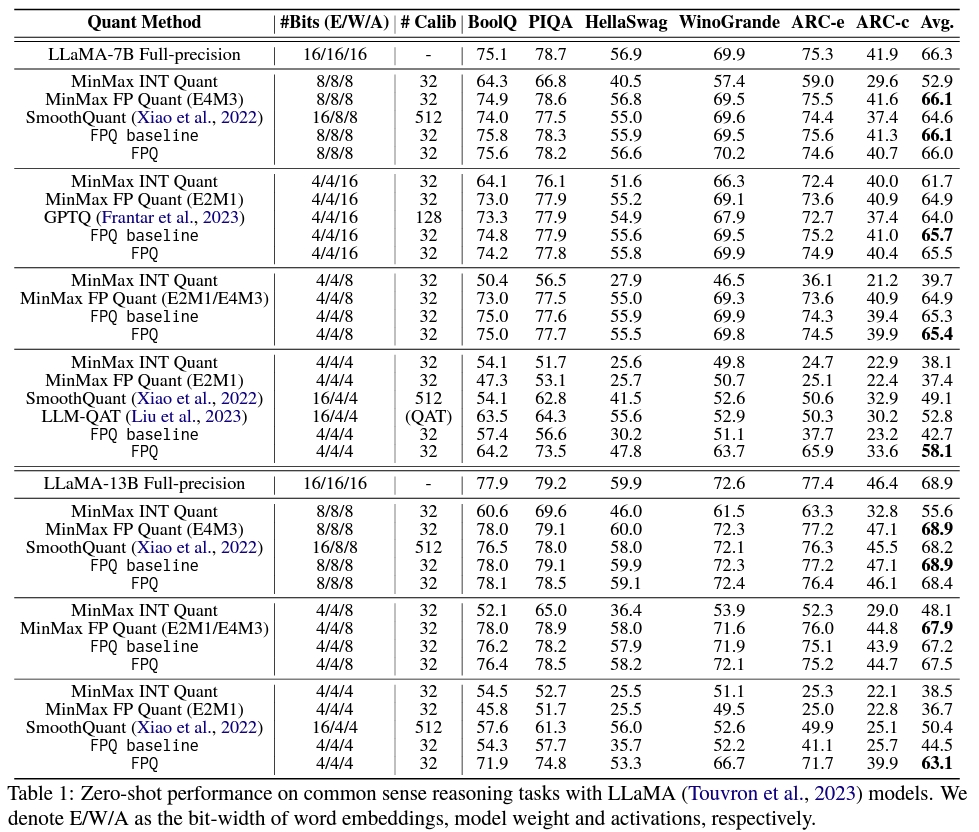
实验结果表明,我们提出的Floating Point Quantization (FPQ) 方法在 LLaMA, BERT 以及 ViTs 模型上,4-bit 量化皆取得了远超 SOTA 的结果。特别是,我们展示了 4-bit 量化的 LLaMA-13B 模型,在零样本推理任务上达到平均 63.1 的分数,只比完整精度模型低了 5.8 分,且比之前的 SOTA 方法平滑量高出了 12.7,这是目前少数已知可行的 4-bit 量化方案了。
参考文献
[1] FP8 Quantization: The Powerof the Exponent, Kuzmin et al., 2022
[2] llm.int8(): 8-bit matrix multiplication for transformers atscale, Dettmers et al., 2022
[3] Smoothquant: Accurate and efficient post-training quantization for large language models ,Xiao et al., 2022
